26. Линеаризованные модели адаптивных систем

Построение координатной модели основного контура и ее линеаризация мало чем отличаются од обычной линеаризации¹ уравнений движения основного контура. Построение параметрической модели регулятора адаптации можно выполнять по схеме, что требует построения модели дли опорного вектора качества Y(t). Линеаризацию полученной модели можно выполнить как обычным путем, так и с использованием методов теории чувствительности. Для этого рассмотрим более подробно структурную схему беспоисковой адаптивной системы.

(8)

Уравнение разомкнутого ОК по отношению к вектору Y преобразуется к виду

(9)

Линеаризованное уравнение относительно опорного режима при малых отклонениях возмущаемых параметров можно преобразовать по Лапласу и оставить в полученных выражениях только те слагаемые разложения нестационарных передаточных функций в ряд Заде, которые соответс- твуют квазистационарным членам

(10)

где — квазистационарное решение; Ф и Ф — матричные передаточные функции по управляющему и возбуждающему воздействиям.

Запись переменных в правой части уравнения нужно понимать в следующем смысле: изображение вектора вычисляется по матрицам Ф и Ф₍, «замороженных» в момент t = передаточных функций.

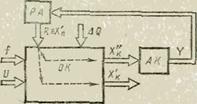
Рисунок 9-Структурная схема беспоисковой адаптивной системы управления.

Уравнение координатно-параметрической модели регулятора адаптации относительно приращения вектора качества б Y приведено в виде

(11)

— составляющая вектора 6Y, обусловленная координатами возмущениями относительно опорного режима U, ; Y —

составляющая Y, обусловленная параметрическими воздействиями

Q, R; _aY —составляющая, обусловленная аппроксимацией

модели основного контура высокого порядка моделью низкого

"порядка. Эта последняя составляющая может отсутствовать

Для построения параметрической модели РА (рис.9) выделим составляющую Y, которую для простоты обозначим Y. Считая координатные возмущения равными нулю, получаем

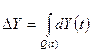(12)

где интеграл берется по траектории изменения параметров Q (t),

R (t)/