21. Статические характеристики адаптации и линеаризованные модели адаптивного регулятора с эталонной моделью

Проводя преобразования структурной схемы связной линеари­зованной адаптивной системы управления, получаем схемы коор­динатного (рис. 11, а) и параметрического (рис. 11, б) каналов. На  рис. 11   F₁ и F₂ — собственные  приведенные  координатные возмущения,  F₁ и F₂ — приведённые координатные возмущения соседних каналов ;

                                                   

                                                 

                      а индекс «В» означает варьированное значение переменной.

Входы каналов обо­значены точками / и 3, а их выходы (в прира­щениях соответствую­щих координат) — точ­ками 2 к 4. Структур­ные схемы изображены в таком виде, который позволяет каждый ра­зомкнутый канал двух­мерной системы предста­вить в виде последова­тельного соединения структуры изолированного разомкнутого канала и так называемой присоединенной структуры, которая не содержит элементов структуры изолированного канала, за исклю­чением элементов, общих для обеих структур. Присоединенные структуры выделены пунктирной линией и полностью характери­зуют влияние, оказываемое связью через соседний канал, на дина­мические характеристики рассматриваемого канала.

Соответствующие указанным структурам присоединенные пере­даточные функции V(s) (канал 1) и V₁₁ (в) (канал //) позволяют выяснить те новые свойства динамических характеристик обоих каналов,  которые обусловлены их взаимосвязью.

 

 

 

 

 

 

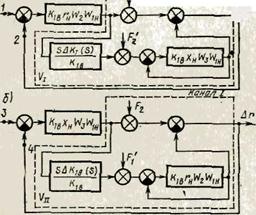
Рисунок 11-Структурные схемы координатного (а) и параметрического (б) каналов с учётом связей через соседние каналы

На основании структурных схем каналов (рис. 11) можно со­ставить следующие выражения для передаточных функций V и V

                                    (14)

                                   (15)

Вследствие того что коэффициент усиления в каждом канале заранее не известен, удобно строить семейства присоединенных частотных характеристик, зависящие от двух параметров: значения коэффициента усиления разомкнутого изолированного канала и относительной вариации параметра а. При этом количество необхо­димых вычислений можно сократить, если значение шага варьи­руемого коэффициента усиления принять равным величине а.